[JAVA] 백준 11054. 가장 긴 바이토닉 부분 수열

이 글은 읽는데 약 6분이 걸립니다.

※개인 공부 목적의 정리글입니다.
이 글의 내용이 최선의 해답은 아닐 수 있습니다.

문제

403 Forbidden
www.acmicpc.net

수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < … Sk-1 < Sk > Sk+1 > … SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.

예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만,  {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다.

수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)

출력

첫째 줄에 수열 A의 부분 수열 중에서 가장 긴 바이토닉 수열의 길이를 출력한다.

바이토닉 수열이란

먼저 문제에 나오는 바이토닉 수열에 대해 알 필요가 있다. 간단히 설명하면 증가하다가 감소하는 수열이다.

예시로 보자. {1, 2, 3, 4}는 증가만 하므로 증가 수열이다. {4, 3, 2, 1}은 감소만 하므로 감소 수열이다.

{1, 2, 4, 6, 4, 2, 0}은 증가하다가 감소하므로 바이토닉 수열이다. 이 때 증감의 크기는 상관없다. 1씩 커지다 3씩 커져도 어쨌든 증가하는 것이다. 감소할 때도 마찬가지.

다만 {1, 2, 2, 4, 5, 3, 2, 1}처럼 같은 수가 연속으로 나오면 안된다. 증가하는 것도 아니고 감소하는 것도 아니기 때문이다.

문제는 주어진 수열에서 찾을 수 있는 가장 긴 바이토닉 수열의 길이를 묻고있다.

풀이

이전 문제인 11053. 가장 긴 증가하는 부분 수열을 풀어보았다면 생각보다 쉽게 풀 수 있다.

[JAVA] 백준 11053. 가장 긴 증가하는 부분 수열
※개인 공부 목적의 정리글입니다.이 글의 내용이 최선의 해답은 아닐 수 있습니다. 문제 수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, ...
yuria.dev
2023.10.22

사실상 이 문제와 푸는 방식이 거의 같으므로 풀어보지 않았다면 한번 보고오자.

일단 주어진 수열로 부터 증가하는 부분 수열의 각 길이를 구한다. 그리고 반대로 감소하는 부분 수열의 각 길이를 구한다. 감소하는 부분 수열의 각 길이를 구하기 위해서는 간단히 증가 구할 때의 반대로 배열을 탐색하면 된다.

※dpinc = dp increase

이 표는 주어진 수열 arr에 대해서 각 숫자까지 증가하는 수열의 길이를 모두 나타낸 것이다.
예시로 arr[5]까지 증가하는 부분 수열의 길이는 {1, 2, 3}으로 3이다.

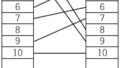
※dpinc = dp decrease

반대로 이 표는 주어진 수열 arr에 대해서 각 숫자까지 감소하는 수열의 길이를 모두 나타낸 것이다.
위 화살표는 배열의 탐색 방향 및 값이 채워지는 방향을 나타낸 것이다.

예시로 dpdec[4]의 값이 의미하는 것은 arr[9] 부터 arr[4]까지 증가하는 부분 수열이 {1, 2, 3, 4}로 길이가 4라는 뜻이다.

이것을 다르게 생각하면 dp[i]는 arr의 i번부터 끝까지에 대해 감소하는 부분수열의 최대 길이를 뜻한다.

이제 두 표를 합쳐봤다. 6번 인덱스(노란색으로 칠한 부분)에 대해서 그 값인 4까지 증가하는 부분 수열의 최대 길이는 {1, 2, 3, 4}로 4이며, 감소하는 부분 수열의 최대 길이는 {4, 2, 1}로 3이다.

여기서 두 값을 더하면 4+3=7이다. 다만 기준이 되는 값인 4가 겹쳐져 계산된것이다. {1, 2, 3, 4, 4, 2, 1} 이런 식으로 중간에 4가 두 번 들어가서 총 7번이 된 것이므로 1을 빼서 중복을 제거해준다.

그렇게 하면 {1, 2, 3, 4, 2, 1}로 6번이 된다.

이걸 그대로 코드로 옮기면 된다.

코드

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
sb = new StringBuilder();

int N = Integer.parseInt(br.readLine());
String[] inputs = br.readLine().split(" ");

int[] arr = new int[N+1];  // 주어지는 수열 입력
int[] dpinc = new int[N+1];  // 증가하는 수열 길이 저장
int[] dpdec = new int[N+1];  // 감소하는 수열 길이 저장
for(int i=1; i<=N; i++){
    arr[i] = Integer.parseInt(inputs[i-1]);
}

dpinc[1] = 1;
dpdec[1] = 1;

for(int i=2; i<=N; i++){  // 증가하는 수열 길이 구함
    dpinc[i] = 1;

    for(int j=0; j<i; j++){
        if(arr[j] < arr[i] && dpinc[i] <= dpinc[j]){
            dpinc[i] = dpinc[j] + 1;
        }
    }
}

for(int i=N; i>=0; i--){  // 감소하는 수열 길이 구
    dpdec[i] = 1;

    for(int j=N; j>i; j--){
        if(arr[j] < arr[i] && dpdec[i] <= dpdec[j]){
            dpdec[i] = dpdec[j] + 1;
        }
    }
}

int result = -1;
for(int i=1; i<=N; i++){  // 두 수열의 값을 합친 후 1을 뺀 값들 중 최대값 구함
    int tmp = dpinc[i] + dpdec[i] - 1;
    if(result < tmp){
        result = tmp;
    }
}
sb.append(result);

System.out.println(sb.toString());
br.close();

감소하는 수열의 길이를 구할 때는 이렇게 그냥 주어진 수열을 뒤에서부터 탐색하면 된다.

댓글