※개인 공부 목적의 정리글입니다.
이 글의 내용이 최선의 해답은 아닐 수 있습니다.
문제
두 자연수 A와 B에 대해서, A의 배수이면서 B의 배수인 자연수를 A와 B의 공배수라고 한다. 이런 공배수 중에서 가장 작은 수를 최소공배수라고 한다. 예를 들어, 6과 15의 공배수는 30, 60, 90등이 있으며, 최소 공배수는 30이다.
두 자연수 A와 B가 주어졌을 때, A와 B의 최소공배수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 1,000)가 주어진다. 둘째 줄부터 T개의 줄에 걸쳐서 A와 B가 주어진다. (1 ≤ A, B ≤ 45,000)
출력
첫째 줄부터 T개의 줄에 A와 B의 최소공배수를 입력받은 순서대로 한 줄에 하나씩 출력한다.
풀이
단순히 두 수의 최소공배수를 구하는 문제이다. 직접 풀면 쉽지만 이걸 어떻게 코드로 구현해야할까?
기존에 우리가 풀 때 사용하는 방법을 그대로 옮길 수도 있겠지만 이미 최대공약수를 구하는 알고리즘이 있다.
우리가 구해야 하는건 최소공배수 아니었나? 최대공약수를 알면 최소공배수도 구할 수 있다. 한번 알아보자.
최소공배수와 최대공약수의 관계
두 수와 최소공배수, 최대공약수 사이의 관계에 대해 알아보자.
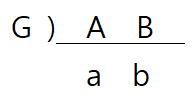
위는 두 수 A, B의 최소공배수와 최대공약수를 구할 때 쓰는 방법이다. \(G\)는 최대공약수(Greatest common divisor)를 의미한다.
당연히 최소공배수 \(L\)(Least common multiple)는 \(G \times a \times b\)이다.
여기서 \(A = G \times a\), \(B = G \times b\)임을 알 수 있다. 즉, \(A \times B = G \times G \times a \times b\)이며, \(L = G \times a \times b\)이므로, \(A \times B = G \times L\)이다.
결국 두 수 A와 B의 곱은 두 수의 최대공약수와 최소공배수의 곱과 같다는 것이다.
정리…
\( L = G \times a \times b\\ A = G \times a\\ B = G \times b\)
\(A \times B = G \times G \times a \times b\\ A \times B = G \times L \)
이로서 우리는 최대공약수만 구하면 최소공배수는 간단한 연산으로 구할 수 있음을 알 수 있다.
최대공약수 구하기 – 유클리드 호제법
최대공약수를 구하는 데에는 유클리드 호제법이라는 알고리즘을 사용할 수 있다. 호제(互除)는 서로(互) 나눈다(除)라는 뜻이다. 왜 이런 이름이 붙었는지는 알고리즘의 실행 과정을 보면 알 수 있다.
두 자연수 a, b(단 a > b)가 있을 때, a를 b로 나눈 나머지 r을 구한다. 만약 r=0이면 그만두고, 아니라면 b를 r로 나누고 그 나머지를 r’라고 한다. 그리고 r을 r’로 나누고…를 반복하면서 결국 나머지가 0이 될 때 까지 반복한다.
나머지가 0이 됬을 때 나누는 수가 바로 최대공약수가 되는 것이다. 글로 설명하면 헷갈리는데, 위키피디아의 유클리드 호제법 문서의 예시 문단을 보면 비교적 알기 쉽게 설명되있다.
그렇다면 이것을 코드로 옮겨야되지 않겠는가? 말은 길어졌지만 코드는 매우 간단하다. 두 수 A와 B 중 더 큰수를 A로 잡아놓는다. 그리고 나머지를 저장할 변수 r도 필요하다.
r이 0이 될 때 까지 루프를 돌리면서 A와 B의 나머지를 r에 저장한 다음, A에는 B의 값을, B에는 r의 값을 저장하면 끝. r=0이 되어 루프가 끝났을 때 A에 저장되어 있는 값이 최대공약수이다.
int A = 12;
int B = 26;
int r = -1;
while(r != 0){
r = A % B;
A = B;
B = r;
}r의 초기값을 -1로 잡은 이유는 만약 0으로 잡으면 while문 조건에 의해 루프가 실행도 안되고 빠지기 때문에 0이 아닌 다른값으로 그냥 -1을 저장해둔 것이다.
코드
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for(int i=0; i<N; i++){
String[] input = br.readLine().split(" ");
int A = Integer.parseInt(input[0]);
int B = Integer.parseInt(input[1]);
int AB = A * B;
// if(A < B){
// int tmp = A;
// A = B;
// B = tmp;
// }
int r = -1;
while(r != 0){
r = A % B;
A = B;
B = r;
}
sb.append(AB / A);
sb.append("\n");
}
System.out.println(sb.toString());
br.close();최대공약수를 구한 다음, 미리 계산해둔 두 수의 곱에 나누면 그것이 최소공배수이다.
두 수의 곱을 미리 저장해둔 이유는 루프를 돌면서 변수 A와 B의 값이 계속 바뀌기 때문이다.
주석처리된 부분은 두 수를 입력받은 후, 더 큰수를 A에 넣는 로직이다만 제출해보면 모든 테스트 케이스에서 A>B인지 저 부분이 없어도 통과된다.


댓글