※개인 공부 목적의 정리글입니다.
이 글의 내용이 최선의 해답은 아닐 수 있습니다.
문제
정수 n(0 ≤ n ≤ 4*109)가 주어졌을 때, n보다 크거나 같은 소수 중 가장 작은 소수 찾는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다.
출력
각각의 테스트 케이스에 대해서 n보다 크거나 같은 소수 중 가장 작은 소수를 한 줄에 하나씩 출력한다.
풀이
문제를 요약하면 각 테스트 케이스의 입력에 대해서, 입력이 소수면 그대로 출력하고 아니면 그 다음 소수를 찾아서 출력하라는 뜻이다.
기본적으로 각 테스트 케이스의 입력이 소수인지 먼저 판별 후, 소수가 아니면 다음 소수를 찾는 방식으로 진행했다.
주의할 점은, 입력의 최댓값이 최대 4,000,000,000 (40억)으로 int의 최대값인 대략 21억보다 크므로 long으로 입력받고 계산해야한다.
제곱근 까지만 검사하여 소수 판별
소수 판별의 경우 가장 기본적인 방법은 2부터 N-1까지 다 나눠보고 만약 하나라도 나누어 떨어지는 수가 있으면 N은 소수가 아닌 것이다.
1과 N은 무조건 나누어 떨어지며, 애초에 소수가 1과 자기 자신으로 밖에 나누어 떨어지지 않는 수이므로 굳이 검사할 필요가 없다.
또한 합성수는 그 수의 제곱근보다 작거나 같은 약수를 갖는다라는 정리가 있으므로, 굳이 제곱근보다 큰 수를 나눠볼 필요는 없다.
public static boolean isPrime(long num){
if(num == 0 || num == 1) return false;
for(int i=2; i<=Math.sqrt(num); i++){
if(num%i == 0) return false;
}
return true;
}위와 같은 방식으로 소수를 판별할 수 있다. 0과 1은 2부터 검사하는 코드로 판별이 제대로 안되므로 따로 처리해준다.
public static long getNextPrimeNum(long num){
num++;
while(!isPrime(num)){
num++;
}
return num;
}다음 소수를 찾는 것은 위와 같이 간단히 구현했다. 먼저 이미 num이 소수가 아닌것이 판별났으므로 num을 1증가시키고 소수인지 판별한다. 소수가 아니면 또 1 증가 시키고 검사하기를 소수가 나올 때 까지 반복한다.
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for(int i=0; i<N; i++){
long num = Long.parseLong(br.readLine());
if(isPrime(num)){
sb.append(num);
}else{
sb.append(getNextPrimeNum(num));
}
sb.append("\n");
}
System.out.println(sb.toString());
br.close();
}
public static boolean isPrime(long num){
if(num == 0 || num == 1) return false;
for(int i=2; i<=Math.sqrt(num); i++){
if(num%i == 0) return false;
}
return true;
}
public static long getNextPrimeNum(long num){
num++;
while(!isPrime(num)){
num++;
}
return num;
}
}내가 짠 코드는 위와 같다.

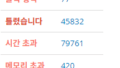
대략 360ms가 걸렸다. 만약 제곱근까지 확인하는 것이 아니라 전체를 그냥 다 확인한다면??

시간 초과가 뜬다.
BigInteger사용
자바에는 BigInteger라는 것이 있다. 이것은 숫자를 문자열 방식으로 저장하기 때문에 사실상 담을 수 있는 수의 크기에 제한이 없다고 봐도 된다.
심지어 소수 판별 및 다음 소수를 찾는 메소드도 제공하고 있어 편하게 풀 수는 있다.
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for(int i=0; i<N; i++){
String num =String.valueOf(br.readLine());
BigInteger bi = new BigInteger(num);
if(bi.isProbablePrime(10)){
sb.append(num);
}else{
sb.append(bi.nextProbablePrime());
}
sb.append("\n");
}
System.out.println(sb.toString());
br.close();
}isProbablePrime() 메소드가 소수를 판별하는 메소드이다. 매개변수로 10을 줬는데, 공식 도큐먼트의 공식에 대입하면 소수일 확률이 나오는데, 10을 넣으면 \(1 – {1 \over 1024} = 0.9901… \)로 거의 확실하다.
그냥 10으로 둔다고 생각하면 된다.
nextProbablePrime() 메소드는 다음 소수를 반환한다.

위가 BigInteger를 사용, 아래가 제곱근 소수 판별법을 사용한 것이다.
BigInteger를 사용하면 코드는 짧고 편해지지만 속도와 메모리 소비가 많아진다.
개인적으로는 그냥 구현이 가능한데 굳이 BigInteger를 쓸 필요는 없다고 생각한다.
댓글