[JAVA] 백준 2164. 카드2

※개인 공부 목적의 정리글입니다.
이 글의 내용이 최선의 해답은 아닐 수 있습니다.

문제
입력
출력
풀이
1. 큐를 사용하기
2. 공식을 만들기
속도비교

문제

N장의 카드가 있다. 각각의 카드는 차례로 1부터 N까지의 번호가 붙어 있으며, 1번 카드가 제일 위에, N번 카드가 제일 아래인 상태로 순서대로 카드가 놓여 있다.

이제 다음과 같은 동작을 카드가 한 장 남을 때까지 반복하게 된다. 우선, 제일 위에 있는 카드를 바닥에 버린다. 그 다음, 제일 위에 있는 카드를 제일 아래에 있는 카드 밑으로 옮긴다.

예를 들어 N=4인 경우를 생각해 보자. 카드는 제일 위에서부터 1234 의 순서로 놓여있다. 1을 버리면 234가 남는다. 여기서 2를 제일 아래로 옮기면 342가 된다. 3을 버리면 42가 되고, 4를 밑으로 옮기면 24가 된다. 마지막으로 2를 버리고 나면, 남는 카드는 4가 된다.

N이 주어졌을 때, 제일 마지막에 남게 되는 카드를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 정수 N(1 ≤ N ≤ 500,000)이 주어진다.

출력

첫째 줄에 남게 되는 카드의 번호를 출력한다.

풀이

두 가지 방법으로 풀 수 있다. 일단 알고리즘 분류부터 큐가 들어있는 것처럼 큐를 이용하면 간단하게 풀어낼 수 있다.
그러나 N에 따른 규칙을 찾은 후 그것을 공식으로 만들어 오직 계산만 해서 바로 답을 찾아낼 수도 있다.
두 방법 모두 설명한다.

문제에서 하는 행동은 이렇다. 1번이 제일 위로 오도록 카드 탑을 순서대로 쌓는다.
이후 탑의 제일 위의 카드를 아예 버린다. 그리고 그 상태에서 제일 위에 있는 카드의 위치를 탑의 제일 아래로 옮긴다.

이것을 카드가 한 장이 남을 때 까지 계속 반복한다.

큐를 사용하기

큐는 선입선출이다. 문제에서 카드 탑을 이용해서 설명하여서 살짝 헷갈릴 수 있는데, 아래 그림을 보자

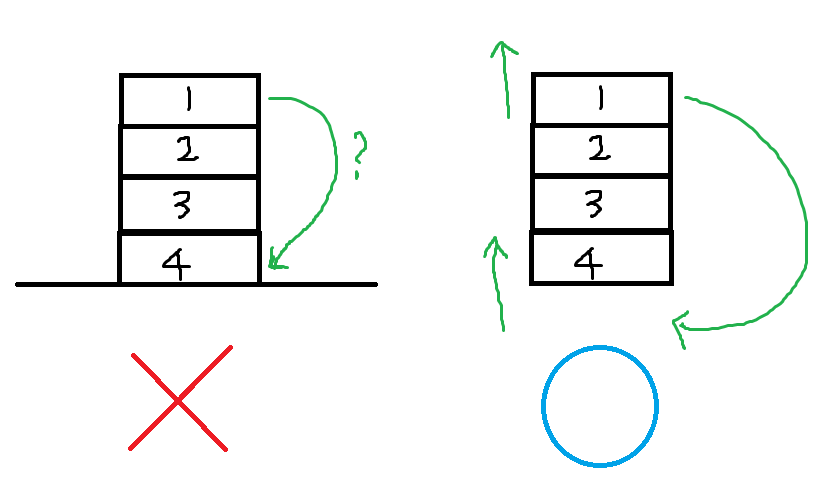
탑이라니 뭔가 바닥에 쌓여있어서 맨 위의 카드가 제일 아래로 가는게 되나? 싶지만 카드 탑이 공중에 떠있다고 생각하면 이해된다. 제일 위의 1을 빼고 다시 넣으면 1은 큐의 제일 뒤인 4의 뒤로 이동한다. 마찬가지로 1부터 큐에 넣었으므로 선입선출에 따라서 1이 가장먼저 빠질 수 있다.

다음으로 문제를 풀기위해 사용할 큐의 메소드를 알아보자. 여기서는 LinkedList를 큐로 이용한다.

remove(): 큐의 가장 첫 번째 값을 삭제한다. (큐 전체 삭제인 clear()와 혼동하지 말자)
poll(): 큐의 가장 첫 번째 값을 반환하면서 삭제한다.
add(n): 큐의 뒤에 값을 추가한다.

이것들만 알면 쉽게 풀린다. 일단 큐에 1부터 N까지 숫자를 집어넣는다. 이후 카드를 빼고 넣을건데, 예시에서 보면 카드가 한 장 남을 때 까지 시행하면 시행 횟수는 N-1회라는 것을 알 수 있다.
N-1번 remove-poll-add를 반복하면 결국 큐에는 하나의 값만 남게되고, 그 값을 출력하면 된다.

int N = Integer.parseInt(br.readLine());
Queue<Integer> queue = new LinkedList<>();
for(int i=1; i<=N; i++){
    queue.add(i);  // 1부터 N까지 순서대로 큐에 추가
}

for(int i=0; i<N-1; i++){  // N-1번 반복
    queue.remove();  // 제일 윗카드 버림
    int num = queue.poll();  // 다음으로 제일 윗카드를 가져와서
    queue.add(num);  // 큐의 제일 뒤에 넣음
}
sb.append(queue.poll());  // 큐에 값이 하나만 있으므로 그것을 빼와서 출력

System.out.println(sb.toString());
br.close();

공식을 만들기

위 코드를 N을 1부터 적당한 수만큼 돌려서 각 N에 대해 정답이 뭔지 출력한 후 규칙을 찾아보자.
일단 N에 대해 답은 이렇다.

1: 2
2: 2
3: 2
4: 4
5: 2
6: 4
7: 6
8: 8
9: 2
10: 4
11: 6
12: 8
13: 10
14: 12
15: 14
16: 16
17: 2
18: 4
19: 6
20: 8
21: 10
22: 12
23: 14
24: 16
25: 18
26: 20
27: 22
28: 24
29: 26
30: 28
31: 30
32: 32
33: 2
34: 4

왼쪽이 N이고 오른쪽이 답이다. 규칙이 보이는가? 조금 더 알기 쉽게 수를 정리해봤다.

1
2

2 4 n=3~4 log2: 1
2 4 6 8 n=5~8 log2: 2
2 4 6 8 10 12 14 16 n=9~16 log2: 3
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 n=17~32 log2: 4

일단 N이 1과 2일때는 예외적으로 빼두고 \(N \geq 3\)부터 보자.

n=5~8이라는 것은 n이 5, 6, 7, 8일 때 순서대로 왼쪽의 숫자가 마지막에 남은 카드의 번호라는 뜻이다. 예시로 n=7이면 마지막 번호는 6이 되겠다.

log2는 \(\log_{2} N-1\)의 소수점을 버린 값이다. 밑이 2인 로그를 이진 로그라고 하는데, 이걸 쓰는 이유는 밑에서 설명하겠다.

보면 2부터 2의 배수가 나열되는데, 일정한 부분에 따라서 계속 2부터 2의 배수가 나열되며, 나열되는 수의 개수가 늘어난다.

나열되는 숫자의 수를 세어보면 2의 \(\log_{2} N\)제곱 개라는 것을 알 수 있다. 예시로 N=14일 때 \(\log_{2} 14 = 3.807…\)로 소수점을 버린 값은 3이며 \(2^3 = 8\)로, N=14가 속한 구간의 수의 개수는 2부터 16까지 8개임을 알 수 있다.

위에서 알아낸 것들을 이용하여서 마지막 번호를 K라고 했을 때, 계산식은 다음과 같이 나타낼 수 있겠다.

\(K = (N – 2^{\log_{2} (N-1)}) \times 2\)

이진 로그에서 N이 아니라 N-1을 쓰는 이유는 이렇다.
만약 N을 쓴다면 \(\log_{2} 9 = 3.169…\), \(\log_{2} 15 = 3.906…\)이고 \(\log_{2} 16 = 4\)가 되는데, 9이상 16이하가 한 구간이므로 한 구간 내에서 정수부분 값이 달라지기 때문에 1을 빼준다.

이로인해 N=9일 경우에는 \(\log_{2} 8 = 3\)로, 어차피 1 빼봤자 정수 부분이 3이니 상관없다.

N에서 해당 구간의 수의 개수를 빼면 구간에서 몇 번째 수인지가 나온다. 여기에 2의 배수이므로 2를 곱하면 답이 나오는 것이다.